雖然內容龐雜,但歸根結底,熱力學的知識其實都可以歸結為四個基本定律:溫度的定義與熱平衡的邏輯、能量守恒在熱學中的體現、自然過程的方向與熵的發現和熱的終點與絕對零度的不可達性。這四個定律不僅奠定了熱力學的基礎,也構成了理解熱現象的邏輯支柱。只要掌握這四大定律,其余內容皆可視為具體條件下的數學推演與物理演繹。
第零定律:溫度的定義與熱平衡的邏輯
在熱力學發展起來之前,人們雖然也有關于冷熱的概念,但對于具體多冷或者多熱,卻無法進行定量的比較。如今被廣泛使用的溫度計,其實也是近幾百年才發展出來的工具。在更早之前,人們很難準確地判斷兩個不同的物體究竟哪一個更熱或者更冷。
比如說有兩個距離遙遠且無法移動的物體A和B,它們的溫度分別是TA和TB,我們要怎么知道它們之間的溫度哪個比較高呢?
這時候如果有一個可以自由移動的物體C,它的溫度為TC,如果用它分別跟A和B進行接觸,結果發現C與A之間、C與B之間都沒有熱量交換(熱平衡狀態),那么我們就可以推斷出:A與B之間也處于熱平衡,即TA=TC=TB,從而TA=TB。
這正是熱力學第零定律的核心思想:如果兩個系統分別與第三個系統處于熱平衡,那么它們彼此之間也處于熱平衡。
該定律不僅為溫度的定義提供了理論基礎,也構建了后續熱力學分析中的測溫邏輯和熱平衡判斷準則。
第一定律:能量守恒在熱學中的體現
工業革命推動了蒸汽機的廣泛使用,也激發了人們對熱能利用效率的深入思考:如何在消耗最少燃料的前提下獲得盡可能多的機械功?在這個背景下,人們意識到,熱量并不是可以憑空生成的,而是與其他形式的能量(尤其是機械功)之間存在轉換關系。

瓦特蒸汽機
這導致了熱力學第一定律的提出,它是能量守恒定律在熱現象中的具體體現:熱量與功是能量的不同表現形式,熱力學系統的內能變化等于系統吸收的熱量減去對外做的功。用數學形式表示為:ΔU=Q?W,其中ΔU為系統內能的變化,Q為系統吸收的熱量,W為系統對外做的功。
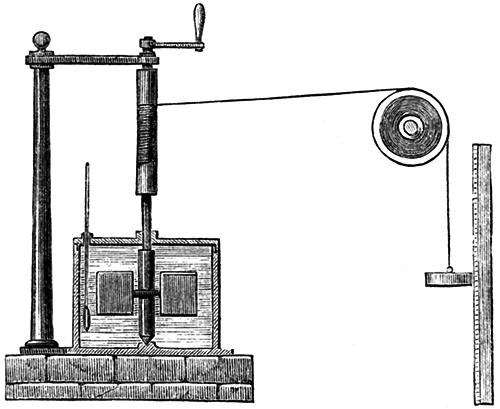
焦耳用于測量熱功等效的設備
第一定律不僅揭示了內能的存在,也直接否定了第一類永動機的可能性,即不消耗能量就持續輸出功的機器是不存在的。
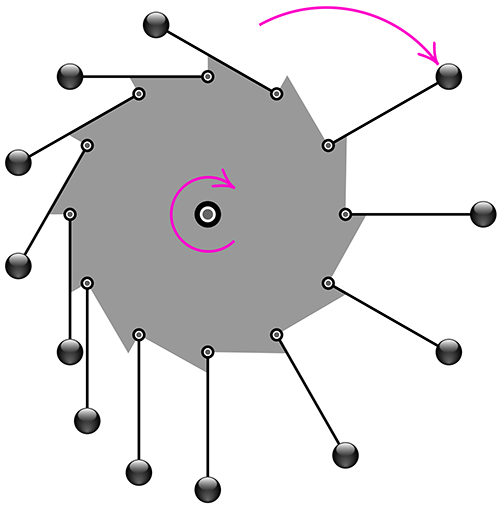
魔輪:歷史上最著名的第一類永動機
第二定律:自然過程的方向與熵的發現
盡管第一定律表明能量守恒,但它并未指明能量轉化的方向性。是否可以將所有吸收的熱量完全轉換為機械功?這一問題引出了第二類永動機的構想:能否設計一種設備,讓它僅從海洋、大氣乃至宇宙中吸取熱能,并將這些熱能完全轉化為有用功?
這一種想法看似有著非常誘人的前景,在歷史上曾經有無數人癡迷于第二類永動機的設計和制造,但終究一無所獲。
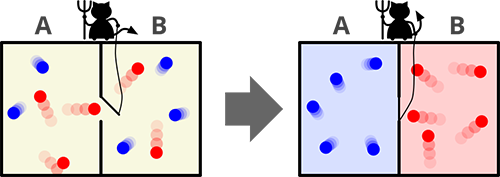
麥克斯韋妖:一個試圖推翻熱力學第二定律的思想實驗
最終人們發現,第二類永動機是不可能實現的,因為熱量不會自發地從較冷的物體流向較熱的物體(克勞修斯表述)。也就是說,不可能從單一熱源吸取熱量,使之完全變為有用功而不產生其他影響(開爾文表述)。
由于熱力學第二定律并不是非常的直觀,除了以上這些表述,還有一些別的等價表述,比如:不可存在一個機器,在循環動作中把一重物升高而同時使一熱庫冷卻(普朗克表述);以及:孤立系統的熵不可能減少(熵增原理)。
對于第二定律更為通俗的理解是:即使在能量守恒的前提下,熱的轉化總伴隨著某種不可逆性。
在熱力學第二定律的發現和發展過程中,卡諾的貢獻功不可沒,他設計出了能提供最大熱效率的卡諾熱機,并且發現:在相同的高溫熱源和低溫熱源間工作的一切可逆熱機的效率都相等,且總是大于不可逆熱機的效率。這就是著名的卡諾定理。
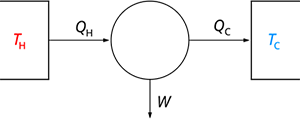
卡諾熱機:只有部分熱量能用于做功,剩余熱量則會流入冷源
第三定律:熱的終點與絕對零度的不可達性
在熱力學第二定律的闡釋中,人們總結出了熵的概念。但熵到底是什么,這一概念曾經讓許多人為之困惑。馮·諾依曼曾經開玩笑說:如果在辯論中以熵作為論據,那你就總能立于不敗之地,因為沒有人知道熵究竟是什么。
隨著對熵這一概念探索的深入,能斯特發現熱力學系統的熵在溫度趨近于絕對零度時將趨于定值,而對于完整晶體而言,這個定值為零,這就是熱力學第三定律。
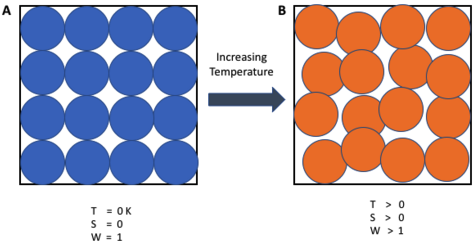
絕對零度下系統只有唯一可能的構型
這一定律不僅為熵賦予了“零點”基準,還揭示了一個極其重要的物理限制:不可能通過有限的步驟使物體溫度降低到絕對零度。
雖然絕對零度(0K,-273.15℃)可望而不可即,但逼近絕對零度的過程也足夠激動人心,不僅液化了各種氣體,還發現了超導、超流等特殊現象,甚至為量子計算奠定了基礎。目前人類可以制造的最低溫度為38pK(0.000000000038K),距離絕對零度僅一步之遙。
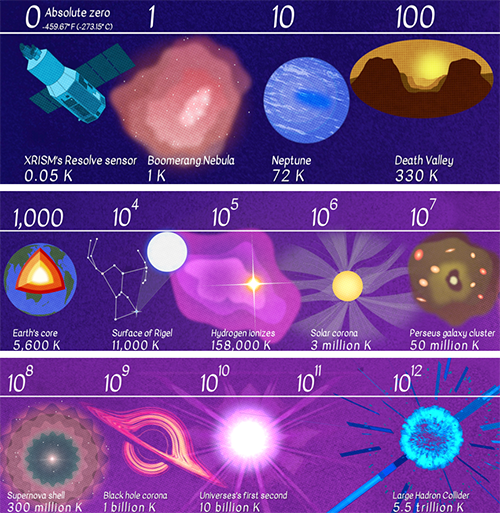
宇宙溫度范圍
相關閱讀
◆溫度計量配套設備之測溫電橋
◆熱力學溫度與攝氏溫度相關知識
◆一文弄懂有效數字與有效數字計算規則







